JEE MAIN CHAPTER OVERVIEW
Chapter Priority | 3 (LOW) |
Number of problems in PYQ | HIGH |
Difficulty | MODERATE/HIGH |
KEY CONCEPTS FOR JEE MAIN
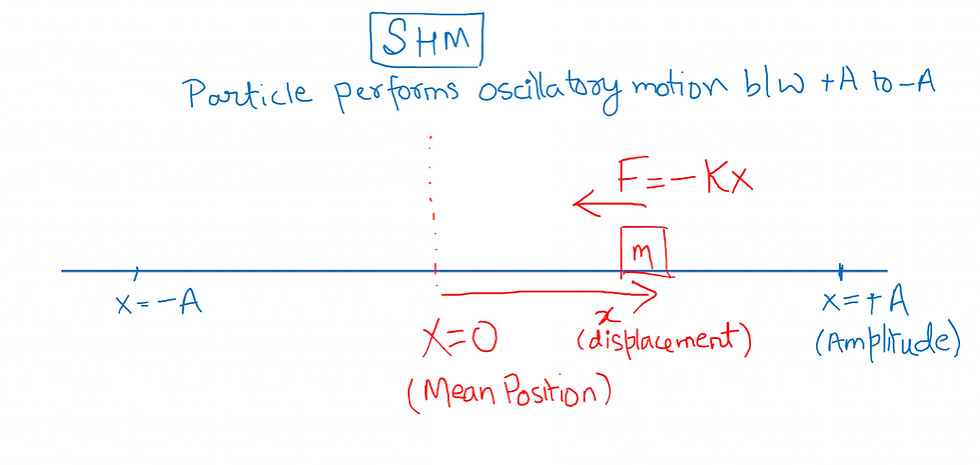
FORCE LAW OF SHM
A particle will perform SHM if it is under a force of the form:
F = -kx
Where k is a constant (also called force constant) and ‘x’ is the displacement of the particle from the mean position.
The particle must have a mean position where Fnet = 0
When displaced in positive direction, force is towards negative direction.
When displaced in negative direction, force is towards positive direction.
If particle has mass ‘m’, both equations below are valid
Therefore,
w is the angular frequency [don’t confuse this with angular velocity of circular motion]
‘a’ is the acceleration of the particle.
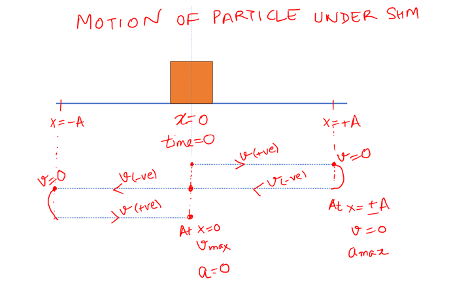
EQUATION OF MOTION UNDER SHM
Where,
‘x’ is the displacement of the particle from mean position
‘A’ is the amplitude (maximum displacement in positive and negative direction)
'w' is the angular frequency [ don’t confuse this with angular velocity of circular motion
'wt' is the angle inside the sin function => It is called ‘phase’ (Phi). Since time always increases, phase (Phi) always increases with time.
RELATION BETWEEN POSITION(X) & PHASE (PHI)
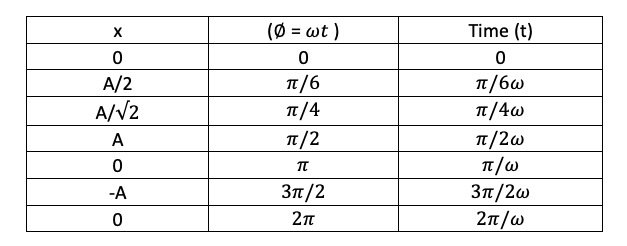
Time period = Time to complete one whole cycle of oscillation
IMPORTANT FORMULAE FOR SHM
TRY JEE MAIN PYQs
Q. A particle executes SHM between x = +A and x = -A. If the time taken by the particle to go from x = 0 to x = A/2 is 2s; then the time taken to go from x = A/2 to x = A is _________
[Hint: Use the phase and position table given above]
Q. A particle of mass 250g executes SHM under a periodic force F = (-25x) N. The maximum speed of the particle is 4 m/s. Find the amplitude of motion.
[Hint: What is the formula for maximum velocity in SHM? v(max)= Aw]
[If you cannot solve, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
ENERGY ASSOCIATED WITH SHM
Total Energy (TE) = Potential Energy (U) + Kinetic Energy (KE)
Therefore,TE is constant [Very important]
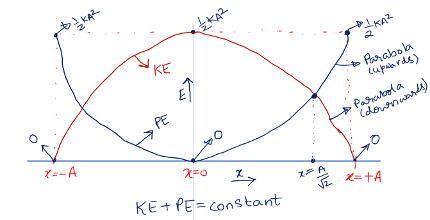
Potential Energy as a function of time is given by the function below
This is useful when JEE MAIN questions asking about relation of energy vs time are asked. For example:
TRY JEE MAIN PYQs
Q. Let T be time period of a particle under SHM, when will the slope of the PE vs Time graph be maximum.
[Hint: Differentiate PE equation w.r.t time to get slope. Maximize the slope, find out the angle (phase) and calculate time to reach that phase.]
[If you cannot solve, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
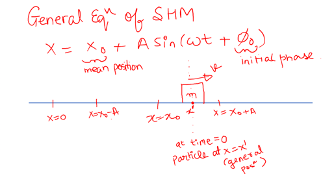
GENERAL EQUATION OF SHM
When the particles mean position is not x = 0 but some x = 0 and at time = 0, the particle starts from a general point x = x’.
EXAMPLES
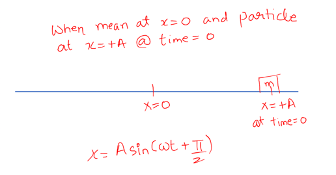

SHM & TIME PERIOD
FORCE METHOD
Steps:
a. Find Mean position where Fnet = 0
b. Displace particle slightly from mean position
c. Write Force on particle expressed in form of F = -kx
In this case, the time period is
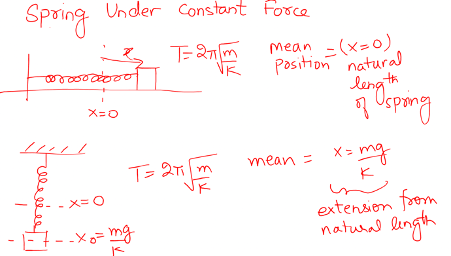
TIME PERIOD OF SPRING UNDER CONSTANT FORCE
Whenever a constant force is applied on a spring, its mean position can differ but time period remains constant.
[m – mass of particle, k – spring constant]
Time period is:
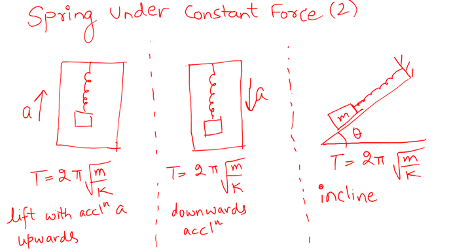
In all cases, mean position will differ but time period will be same. Under acceleration, a constant pseudo force changes mean position but time period is not impacted.
COMMON QUESTION ASKED IN JEE MAIN
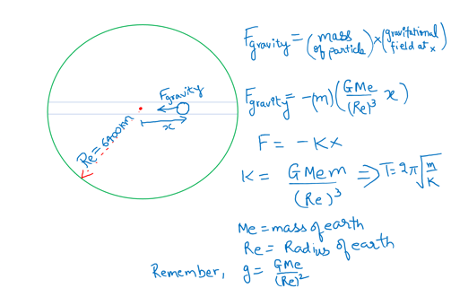
Assume that the earth is a solid sphere of uniform density and a tunnel is dug along its diameter throughout the earth. It is found that when a particle is released in the tunnel, the particle executes SHM. The mass of the particle is 100g. The time period of motion will be (approximately) (take g = 10m/s2, radius of earth = 6400km)
Such a question using gravitation and SHM concepts is very common.
Here,
R = Radius of earth; g = acceleration due to gravity.
Try solving it yourself [Hint: What is the gravitational field at a point inside a uniform solid sphere]
[If you cannot solve, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
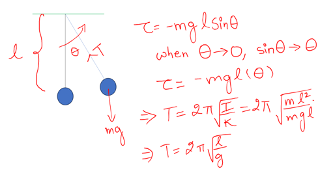
SIMPLE PENDULUM
Simple pendulum is a case of rotational SHM. Given below is the comparison between Linear and Rotational SHM.

For a simple pendulum,
Remember, the ‘g’ in the equation is g(effective).
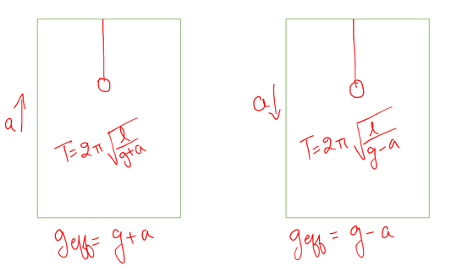
g(effective) – TIME PERIOD
When pendulum inside a lift accelerated (a) upwards
When pendulum inside a lift accelerated (a) downwards
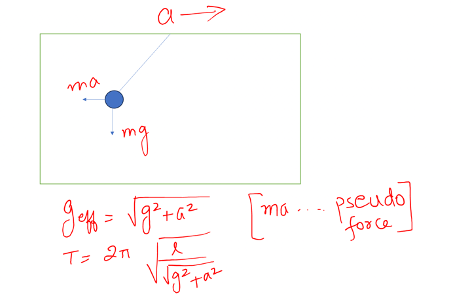
When accelerated horizontally (a)
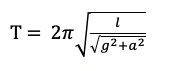
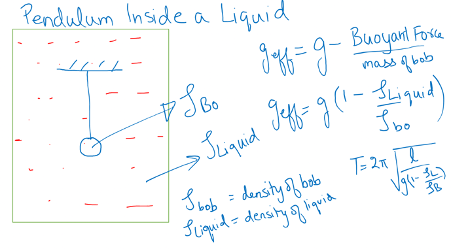
PENDULUM INSIDE A LIQUID
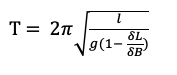
Where is density of liquid and is density of bob attached to pendulum
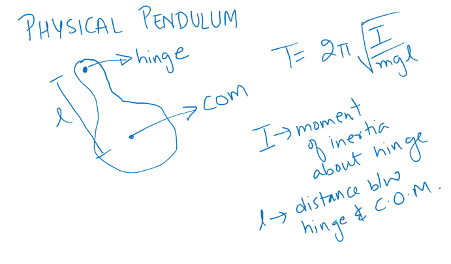
PHYSICAL PENDULUM
In this, remember perpendicular and parallel axis theorems of moment of inertia
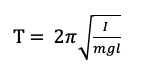
I = moment of inertia about hinge
L = distance of centre of mass from hinge point
Keff
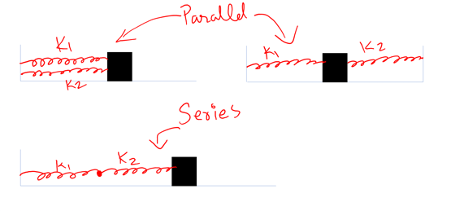
Series combination: (1/Keff) = (1/K1) + (1/K2) + (1/K3)….
Parallel combination: Keff = K1 + K2 + K3…….
PLEASE COMMENT BELOW IF YOU WANT TO SHARE FEEDBACK ON THIS PAGE.
For any kind of doubts or if you require Physics classes visit www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]

Comentários