JEE MAIN CHAPTER OVERVIEW
Chapter Priority | 4th (Lowest) |
Number of problems in PYQ | Low |
Difficulty | Easy/Moderate |
Note: For JEE MAIN, Waves & Sound is formula based. All you need to do is to memorise the formulae and use the correct formula in the questions.
KEY CONCEPTS FOR JEE MAIN
WHAT ARE WAVES?
Waves are a kind of disturbance that travel from one point to another carrying energy.
Keep in mind, a particle inside a wave a does not travel along with the wave. Particle performs an oscillatory motion but does not move away from its mean position.
TYPES OF WAVES
There are two types of waves:
Mechanical Waves - Wave travels through a physical medium. For example, waves on a string, sound waves etc.
Electromagnetic waves - do not require a medium to propagate. For examples , visible light, radio waves, television signals, and x-rays.
We will study mechanical waves in this document.
TRANSVERSE & LONGITUDINAL WAVES
When the particle oscillates perpendicular to the direction in which wave travels, it is a transverse wave.

In the above image, wave travels along +x axis with a speed 'c' while particles oscillate up and down as the waves passes. This results in transfer of energy but not motion in horizontal(x) direction.
When the particle oscillates parallel to the direction in which wave travels, it is a longitudinal wave.

In the above image, wave travels along +x axis while particles also oscillate in x-direction as the waves passes. This results in transfer of energy but not motion in vertical(x) direction.
VARIABLES & TERMS IN WAVE MOTION

For waves, we can define certain terms:
Crest: The point at which the displacement is highest.
Trough: The point at which the displacement is lowest.
Amplitude: The magnitude of the maximum displacement of particle.Can be in either +ve or -ve direction.
Time period (T): Time required for two identical points (such as two crests or two troughs) to pass through a point. It is time complete on cycle of the wave.
Frequency (f): It is the inverse of time period (f = 1/T). It is the number of crests/troughs that pass through a point in one second.
The distance from one crest/trough to the next is called the wavelength (lambda)
Velocity of wave: Wavelength/Time period
[The above formula is very important. Lots of questions are asked in JEE MAIN on this equation alone. Think about how you can play with the above equations:
What will be frequency of wave in terms of velocity of wave & wavelength?
How can you write wavelength in terms of velocity of wave and time period?]
Angular frequency (omega):
Particle performs oscillatory motion a wave. If the wave equation is a sin or a cos function. Then that oscillatory motion of the particle is an SHM. Angular frequency is associated with this SHM. (S.I. units: Radians/second)
Angular Wave Number (k):
[The above formula is very important. Later in this article, we will study phase. Angular wave number relates the distance between two particles and their phase.
Very useful formula for three chapters - Waves, Sound Waves and Wave Optics]
Relation between velocity of wave, angular frequency and wave number:
Velocity of Particle:
Do not confuse this with velocity of wave. It is the velocity with which a particle is moving as it oscillates. (We will see the formula later on in this document).
EQUATION OF WAVE MOTION
Any function can describe the motion of a particle inside a wave if it has three characteristics:
Continuous
Differentiable
Bounded (should not go upto infinity)
We study waves using sin and cos functions because they follow the above rules and are easy to analyse.
In JEE Advanced, a lot of questions give you equations other than sin and cos. So make sure you understand key concepts.
In JEE MAIN, mostly only sin and cos wave equations are asked.
Now, let us study wave equations -
Equation of wave travelling in positive x-direction:
'y' is the vertical displacement of the particle in case of a longitudinal wave.
This equation tells us what is the displacement of a particle a point (x) at a time (t).
For example, what is the displacement of a particle at x = 10m at time = 3s.
By changing 'x', you can get the displacement of all particles at a time 't'.

In the above figure, velocity of wave is v.
Thus, wave moves forward, 'vt' distance in time interval 't'.
Remember,

Equation of wave travelling in negative x-direction
Velocity of particle and Velocity of wave
Now we know displacement of particle.
Vparticle = dy/dt
Which means: Vparticle = -Aw[cos(kx-wt)]
[Note: Above equation is valid when equation of wave is y = Asin(kx - wt)]
There is another equation relating velocity of wave (Vw) and particle(Vp):
dy/dx is the partial differentiation of displacement(y) with position (x).
It gives us the slope of the graph of the wave equation.
TRY JEE MAIN QUESTIONS
Q. A travelling wave is described by the equation:
y(x, t) = [0.05 sin (8x - 4t)] m
The velocity of the wave is: [all the quantities are in SI unit]
[Hint: Use v = w/k]
Q. A transverse wave is represented by y = Asin(ωt – kx). For what value of the wavelength is the wave velocity equal to the maximum particle velocity?
[Hint: If velocity of particle = -Aw[cos(kx-wt)], then max velocity of particle equals Aw]
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
PHASE & PATH DIFFERENCE
Possibly, the most important formula for studying waves and related topics like wave optics. It also helps you understand interference and superposition.
Let us study this is a bit of detail, so you always remember it.
What is phase?
When we study the equations of a wave, we use a sun or a cos function. Within the function is an angle like (kx-wt) or (kx+wt). This angle is called the phase.
Phase is represented by greek letter (phi)
Two particles in a wave are at different positions (example one particle is at x = 3m and while other is at x = 4m). Both these particles have different displacement from mean.

But we know that displacement is given by
y = Asin(phase)
Thus, the two particles at two different positions must have different phase for displacement to be different.
This is called phase difference.
The difference between positions (x1 & x2) is called path difference.
The relation between phase difference and path difference is given by:
[Note: When the path difference between two particles is 1 lambda, then phase difference is 2(pie)]
VELOCITY OF WAVE IN A STRETCHED STRING
Questions are asked on cases where a wave travels in a stretched string. The string has the following properties:
Mass per unit length:
Tension in string is 'T'
Then velocity of wave in the string is:

TRY JEE MAIN QUESTION
A steel wire with mass per unit length 7.0 × 10-3 kg m-1 is under tension of 70 N. The speed of transverse waves in the wire will be?
[Hint: Directly apply the formula]
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
Questions can be asked by varying the tension along the string.
For example, if they hang the string vertically in the question. Tension increases as we go up the string and so the velocity also goes up the string as well.
Question: Small pulse is created at the bottom of the string of mass per unit length μ, which travels upwards. Find the velocity and acceleration as a function of distance from the bottom.

In the above queston, we need to use calculus because Tension varies at each point. You should remember the relationship derived above in case it is asked directly in the JEE MAIN paper.
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
INTENSITY OF A WAVE
It is defined as the energy of the wave passing through a unit area per unit time.
Intensity = (1/2)*(density of medium)*(velocity of wave)[(angular frequency)*(Amplitude)]^2
Remember, Intensity is proportional to square of Amplitude.
REFLECTION OF WAVES
When waves move from one medium to another. A part of the wave moves forward while the other part gets reflected back in to the original medium.
Case 1: Rarer to denser medium

In rarer medium, speed of wave is higher.
When a wave enters a denser medium, the part which is reflected back into rarer medium, changes its phase.
Change in phase of reflected wave in going from rarer to denser medium is
Path difference is
This is called reflection from hard boundary. It is similar to a thread tied to a fixed end and getting reflected wave from it.

Case 2: Denser to rarer medium

In rarer medium, speed of wave is higher.
When a wave enters a rarer medium, the part which is reflected back into denser does not change its phase.
Change in phase of reflected when going from denser to rarer medium is ZERO
Path difference is also ZERO
This is called reflection from soft boundary. It is similar to a thread tied to a free end and getting a reflected wave from it.
In both cases, no phase change occurs for transmitted wave (i.e., the wave that goes forward into the next medium).
SOUND WAVES
Sound waves are longitudinal waves.
As a sound wave passes, the particles in air move back and forth parallel to the direction of the propagation of sound waves.
The equation of waves is similar for both longitudinal and transverse waves.
Keep in mind,
'y' in the above equation is the displacement of the air particle from its mean position. This 'y' will be parallel to the direction of velocity of sound wave.
All formulae relating to k, w(omega), Time period and frequency are still valid.

In longitudinal waves, there are compressions and rarefactions just like there are crests and troughs.
Compression: Particles come close to each other, density increases, pressure increases.
Rarefaction: Particles go far from each other, density decreases, pressure decreases.
In addition to displacement equation, in sound waves we can also write the equation of variation of Pressure with (position and time)
Pressure varies as:
The above equation relates change in pressure (and not absolute pressure)
P0 can be atmospheric pressure or as per data in question.
B = Bulk modulus
A = Amplitude of displacement (from y = Asin(kx-wt))
k = wave number (from y = Asin(kx-wt))
The following equations are also useful:
Change in Pressure is dependent on Bulk Modulus of air
Max Change in Pressure (Pressure Amplitude)
Remember,
If graphs of pressure and displacement are asked -
Displacement varies as a sin function.
Pressure varies as a cos function.
TRY A QUESTION
If difference between max pressure & min pressure at a point is (10)^(–3) Pa. Find displacement amplitude if 𝜆 = 40cm & B = 1.4 × 105 N(m)^(–2).
[Hint: Pmax = P0 + BAk & Pmin = P0 - BAk]
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
INTENSITY OF SOUND WAVES
As discussed earlier,
Now, we know:
v = w/k
Pressure Amplitude is given by:
We can use the above formulae, to get alternate formula for Intensity.

Important: Intensity is proportional to square of Pressure Amplitude (BAk)
SPEED OF SOUND
Speed of sound in Solids depends upon the Young's Modulus and density.
Speed of Sound in liquids and gas is dependent on Bulk modulus and density
NEWTON's FORMULA & LAPLACE's CORRECTION
Newton suggested a formula for speed of sound. This formula was close but not excatly accurate so Laplace corrected it.
Newton assumed sound propagated in an isothermal process.
In isothermal process, Pressure = Bulk modulus.
Newton's Speed of sound can be written as:
But since experimentally it was found to be incorrect. Laplace suggested that sound travels adiabatically.
In adiabatic process, Bulk modulus is given by
With this correction, speed of sound is
We can write density as (Mass/Volume)
and PV = nrt
We will get the formula for velocity of sound as:
M0 is the molecular mass of the gas.
TRY A QUESTION
Q. Find ratio of speed of sound in O2 & He at same temperature.
[Hint: Use appropriate values for gamma & molecular mass of the gases]
Q. Find speed of sound in a mixture of 1mole of He & 2 mole of O2 at 27°C.
[Hint:
]
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
LOUDNESS & PTICH
Loudness is a measure of intensity of sound. More intensity of sound leads to a louder sound.
It is measure in Decibel.
Loudness in Decibels = 10log(I/I0)
Where I0 = 10^(-12) W/(m^2)
Pitch of sound is related to frequency of sound. Higher frequency implies a higher pitch.
SUPERPOSITION OF WAVES
Superposition involves two or more waves that intersect a particular point. The net displacement of a particle is given by the vector addition of the displacements due to each individual wave.
For example, Wave 1 and Wave 2 intersect at a point.
Wave 1: y1 = A1sin(k1x + w1t)
Wave 2: y2 = A2sin(k2x + w2t)
Net displacement: ytotal = A1sin(k1x + w1t) + A2sin(k2x + w2t)
Here, we will use relevant trigonometric identities to simplify the equation as per data in question.
Superposition has three applications for JEE MAIN:
Interference: Relevant for Wave Optics.
Standing Waves
Beats
STANDING WAVES
When two waves with
same speed,
same frequency
same amplitude
travel in opposite directions and intersect, then standing waves are produced.
Equations of two waves travelling in opposite directions with above features can be:
y1 = Asin(kx + wt)
y2 = Asin(kx - wt)
Final equation of wave produced after adding up both y1 & y2 is:
ytotal = 2Asin(kx)cos(wt)
Notice that the above equation does not have any term like (kx-wt) or (kx+wt). This implies that the wave is stationary, i.e., it does not travel along either +x or -x direction. Hence, it is called standing wave. Energy is confined in a region.

Each particle in a standing wave performs an SHM with amplitude that depends only on its position.
Amplitude = 2Asin(kx)
Depending upon the value of 'x', Amplitude for some particles can be ZERO. These points are called NODES.
Amplitude for some particles can be maximum at (2A). These points are called ANTINODES.
Distance between two nodes or two antinodes is half the wavelength (lambda/2).
Distance between a node and next antinode is (Wavelength/4) = (lambda/4)
TRY A QUESTION
Given equation of standing wave is Y = 4 Sin (1.5𝜋x) cos (6𝜋t). Find (i) Equation & velocity of parental waves (ii) Node located closest to origin. (iii) Amplitude of particle at x = 1/3 m
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
STANDING WAVES IN STRINGS & ORGAN PIPE
Standing waves can form in strings with one end open or both ends fixed.
Standing waves can form in organ pipes with one end closed or both ends open.
Both the cases have matching results and should be handled together.

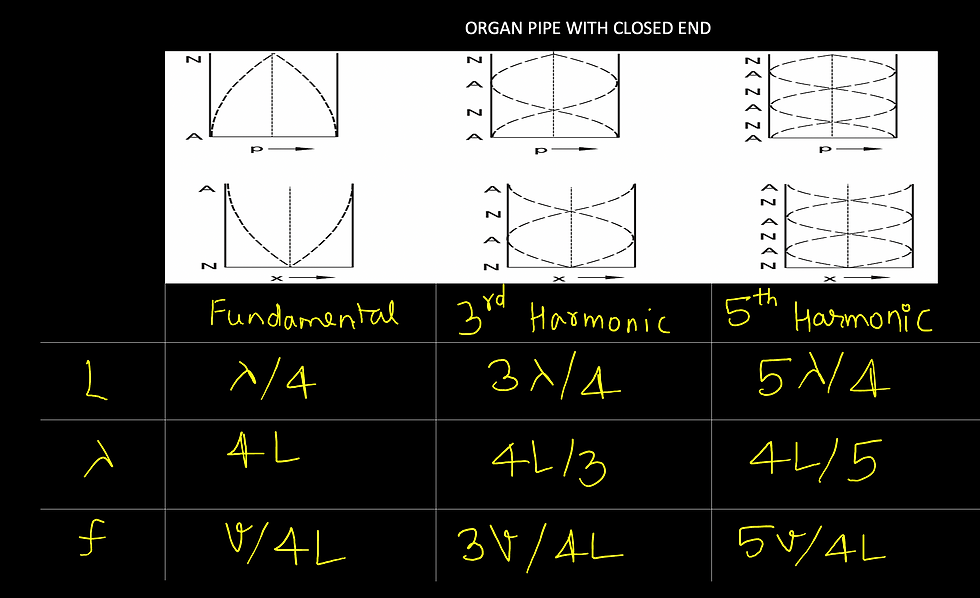



TRY A QUESTION: Q. An open pipe is immersed in water to half its length. The ratio of the fundamental frequency of the pipe before and after immersion in water is?
[Hint: After immersion, open pipe becomes closed at one end]
Q. The two nearest harmonics of a tube closed at one end and open at other end are 220 Hz and 260 Hz. What is the fundamental frequency of the system?
[Hint: Difference between two frequencies is two times the fundamental frequency]
Q. Standing waves are produced in a 10 m long stretched string. If the string vibrates in 5 segments and the wave velocity is 20 m/s, the frequency is?
[Hint: 5 segments is how many wavelengths?]
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
RESONANCE COLUMN EXPERIMENT
This experiment is done to calculate speed of sound
In the resonance column experiment a tuning fork is placed in front of a tube filled with water. Water is slowing taken out of the tube. Height of air inside tube is measured.
The tube acts as a one end closed pipe.
As water slowly comes down, the length of the pipe changes.
First resonance or loudness occurs at a length when -
Frequency of tuning fork = Frequency of first harmonic of one end closed organ pipe.
Frequency of tuning fork = v/4L .............................[Where L = length of air inside tube]
Note: Sometimes value of end corrections are given.
In such case, first resonance occurs at
Frequency of tuning fork = v/4(L+e).......................[Where e = end correction, L = Length air inside tube]

BEATS
When two waves of nearly equal frequency are sumperimposed, then beats are produced.
f(beat) = f1 - f2
f(beat) = beat frequency
f1 = frequency of 1st sound wave
f2 = frequency of second sound wave
Beat frequency is the number of beats per second.
The phenomenon of periodic variation of intensity (loudness) of sound when two sound waves of slightly different frequencies interfere, is called beats.
Questions are asked on beat frequencies when a tuning fork's prongs are waxed or filed. When waxed, then frequency of tuning fork decreases. When tuning fork prong is shaved, frequency increases.
TRY A QUESTION
A tuning fork of frequency 300 Hz produces 5 beat per second, with a tuning fork of unknown frequency. If the turning fork of unknown frequency is loaded with wax, the beat frequency becomes 3 beat per second. Then find the original frequency of the tuning fork.
[Hint: What is beat frequency in this case? Figure out if the unknown frequency is higher or lower than the known frequency of 300Hz]
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
DOPPLER EFFECT
The phenomenon of apparent change in frequency of the wave received by observer due to motion of the source or the observer is called the Doppler effect.
All you need to do is learn one single formula as given below. When directions change, apply signs accordingly.
Example:
When source moves towards observer, Vs>0 and therefore the denominator (V-Vs) < V. Thus, the frequency received increases.
When observer moves away from source, Vo<0 and therefore the numerator (V+Vo)<V/ Thus, the frequency received decreases.

Try the following question. This is one of the finest questions in Doppler Effect and Beats.
A car is moving towards a wall with velocity Vc. One top of the car is a loudspeaker.Find the Beat frequency heard by the Driver of Car?
[Hint: The beat frequency is due to the driver getting sound waves directly from the loudspeaker and also from the reflected sound wave from the wall.]
[If you cannot solve on your own, let us know your doubt at www.savai.co.in or WhatsApp me @ 7982286138, we will send solution.]
If you want to get in touch for guidance related to JEE, career etc. I am always available at the at www.savai.co.in or WhatsApp me @ 7982286138
Do let us know if you have any feedback.
Please share www.savai.co.in in case you find our content helpful.]

Comments